圆幂定理
目录
弦切角定理
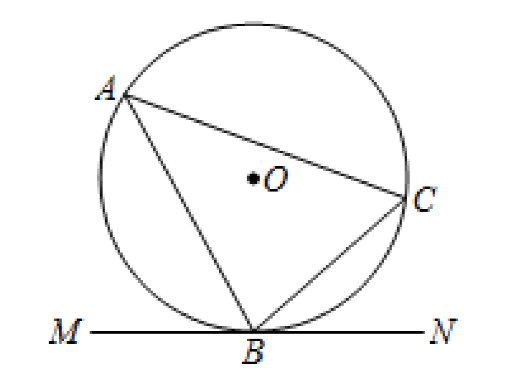
顶点在圆上,一边和圆相交,另一边和圆相切的角叫做弦切角.
弦切角定理:弦切角的度数等于它所夹的弧的圆心角度数的一半。 等于它所夹的弧的圆周角度数。
已知:⊙O是△ABC的外接圆,过点B作⊙O的切线MN,∠A,∠C即为弦切角.
切割线定理
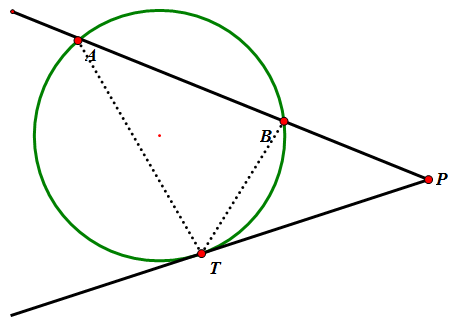
设ABP是⊙O的一条割线,PT是⊙O的一条切线,切点为T,则PT²=PA·PB。
证明
连接AT, BT。
∵ ∠PTB=∠PAT(弦切角定理);∠APT=∠TPB(公共角);
∴ △PBT∽△PTA(两角对应相等,两三角形相似);
∴PB:PT=PT:AP;
即:PT²=PB·PA。
割线定理
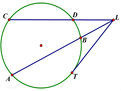
文字表达:从圆外一点引圆的两条割线,这一点到每条割线与圆交点的距离的积相等。 数学语言:从圆外一点L引两条割线与圆分别交于A.B.C.D 则有 LA·LB=LC·LD=LT²。 几何语言:∵割线LDC和LBA交于圆O于ABCD点 ∴LA·LB=LC·LD=LT² 如图1所示。(LT为切线)
相交弦定理
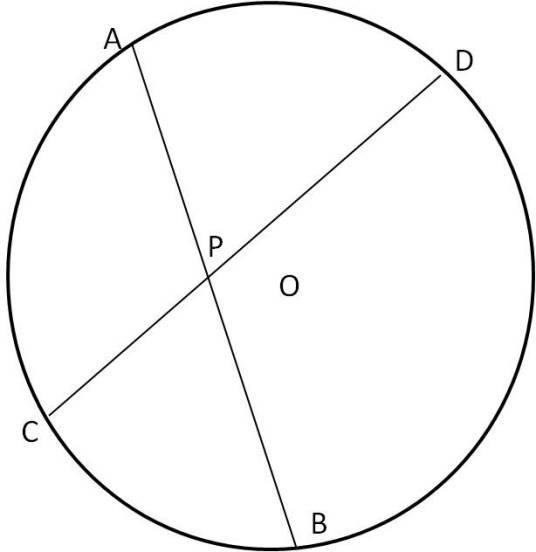
几何语言:
若圆内任意弦AB、弦CD交于点P
则PA·PB=PC·PD(相交弦定理)
托勒密定理
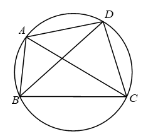
在四边形ABCD中,若A、B、C、D四点共圆,则AC·BD=AB·CD+AD·BC.
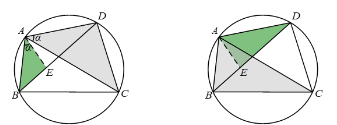
证明:在线段BD上取点E,使得∠BAE=∠CAD,
易证△AEB∽△ADC,
∴AB:AC=BE:CD,即AC·BE=AB·CD,
当∠BAE=∠CAD时,可得:∠BAC=∠EAD,
易证△ABC∽△AED,
∴AD:AC=DE:CB,即AC·DE=AD·BC,
∴AC·BE+AC·DE=AB·CD+AD·BC,
∴AC·BD=AB·CD+AD·BC.
推广(托勒密不等式):对于任意凸四边形ABCD,AC·BD≤AB·CD+AD·BC
米勒最大张角定理
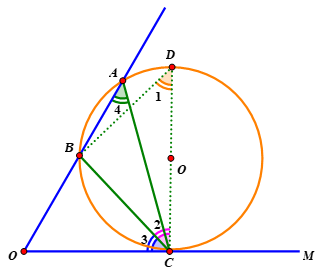
已知点AB是∠MON的边ON上的两个定点,点C是边OM上的一动点,则当且仅当三角形ABC的外接圆与边OM相切于点C时,∠ACB最大。